A D’Hondt-módszer
nem is olyan bonyolult...
A pártlistás arányos választási rendszerek fő két szakaszban osztják ki a mandátumokat:
Először elosztják azokat a listák (pártok) között, majd
Az egyes pártokra jutó mandátumokat kiosztják az egyes jelölteknek
De pontosan hogyan osztják el pártok között a mandátumokat? Erre mutatok be egy gyakori módszert, ami Victor D’Hondt belga jogász-matematikus nevét viseli, de már jóval korábban Thomas Jefferson is feltalálta.
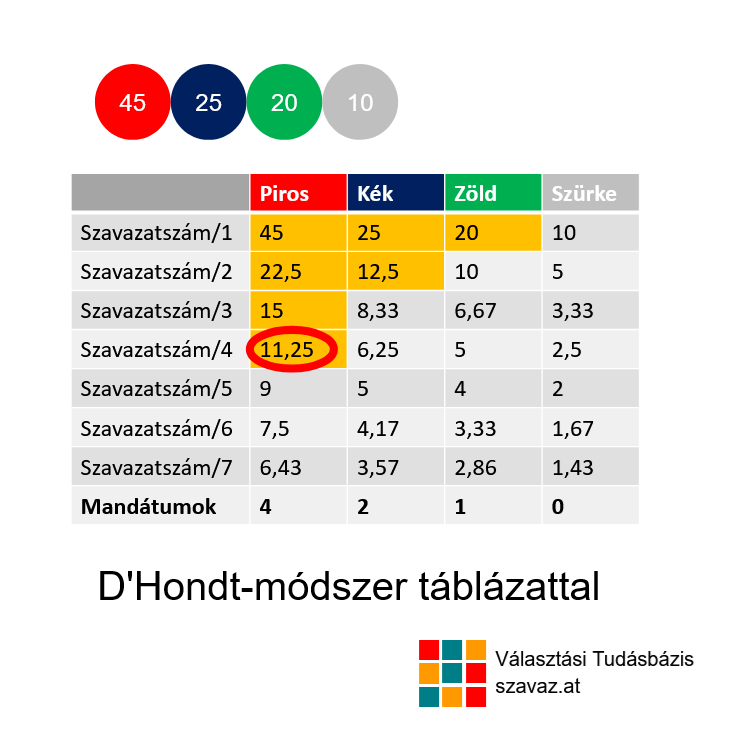
A D’Hondt módszer nem bonyolult: Annyit kell tenni, hogy az egyes pártok szavazatszámát fel kell írni egy táblázat felső sorába, majd az alatta levő sorokba a szavazatszámok felét, harmadát, negyedét stb. Ez látható a képen:
Ezután egyesével ki lehet osztani a mandátumokat, mindig a táblázat legnagyobb számát kell kiválasztani (azok közül, amit még nem választottunk ki). Ezt addig kell ismételni, amíg az összes mandátumot ki nem osztottuk. Azaz, ha k mandátumot akarunk kiosztani, akkor a k legnagyobb számot bejelöljük, majd minden oszlopban összeszámoljuk mennyit jelöltünk be, és mivel minden párt egy oszlop, ezzel meg is kaptuk melyik mennyi mandátumot szerez.
A példában 100 szavazat 4 párt között oszlik meg. Ha 7 mandátumot akarunk kiosztani (emiatt azt is tudjuk, hogy max. 7 sorra lesz szükségünk) a 4 párt között a 7 legnagyobb számot választjuk ki - ez a képen sárgával látszik.
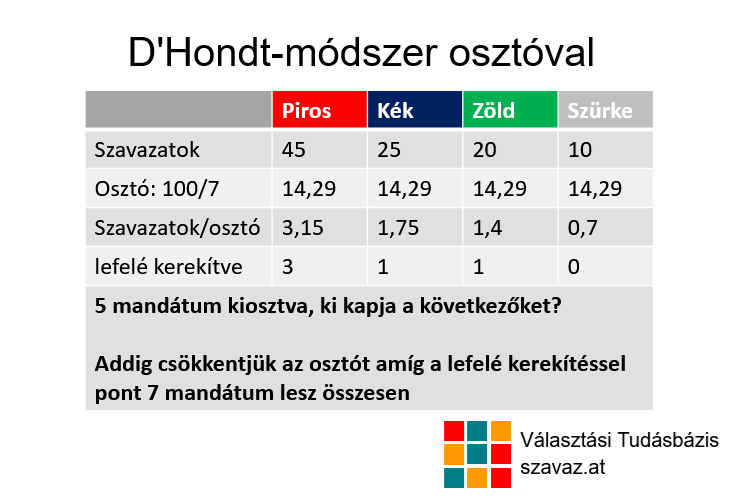
A D’Hondt módszert megfogalmazhatjuk úgy is, hogy minden párt szavazatait ugyanazzal az osztóval leosztva akarjuk megtalálni, hogy mennyi mandátumot szerezzenek. Logikus lenne, hogy ez az osztó az összes szavazat és az összes mandátum hányadosa legyen, vagyis a példában 100/7 = 14,29. De ha ezzel leosztjuk a szavazatokat, nem kerek számokat kapunk. A D’Hondt módszerben (más osztó módszerektől eltérően) mindig lefele kerekítünk. Ha így ki tudjuk osztani az összes mandátumot, akkor ezzel vége is a folyamatnak. De mi van, mint például itt, hogyha a lefelé kerekítéssel nem osztottuk ki az összes mandátumot? A válasz a D’Hondt módszer szerint, hogy az osztót addig csökkentjük, amíg ezzel a lefelé kerekítéssel pont a tervezett mandátumszámot ki tudjuk osztani.
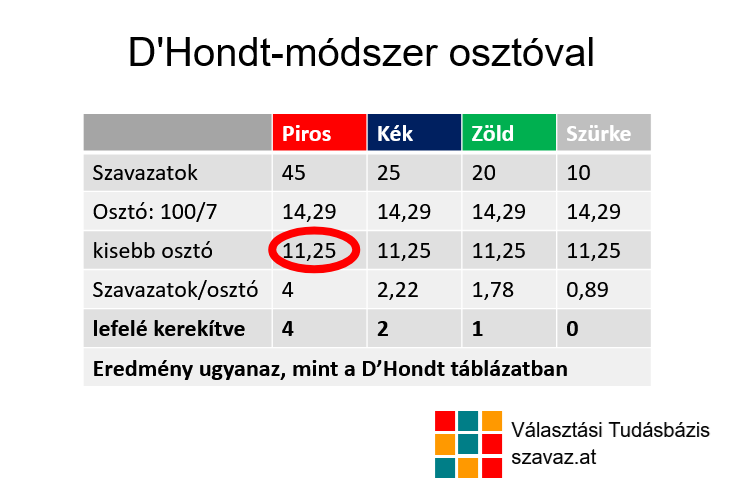
A példában így az osztót (14,29) egészen 11,25-ig kell levinni, hogy a lefelé kerekítéssel 7 mandátumot oszthassunk ki (pl. 11,26 esetén még csak 6-ot osztanánk ki). Ez a 11,25 onnan lehet ismerős (az első és harmadik képen piros körökkel jelölve), hogy pont ez a 7. legnagyobb szám, amivel a D’Hondt táblázatban az utolsó mandátumot megtaláltuk! Ezért ekvivalens a két módszer. Az eredeti 14,29-es osztót nem látjuk a táblázatban, de tudjuk, hogy ennél az értéknél a kerekítéssel 5 mandátumot tudunk csak kiosztani, és lám, a táblázatban is 5 ennél nagyobb (vagy egyenlő) szám van. A 6. mandátumot akkor osztjuk ki, amikor (a nagyobb számok felől jövet) elérjük a 12,5-et, ezt a mandátumot a táblázatunk szerint a kék kapta, és természetesen, ez a 6. legnagyobb szám.
A D’Hondt módszer (és tágabban az osztó-módszerek) a táblázatban egyesével adják a mandátumokat: A példában az elsőt a piros, a másodikat a kék, a harmadikat megint a piros, a negyediket a zöld stb. kapja. Ez azt jelenti, ha 7 helyett úgy döntünk, inkább 8 mandátumot akarunk elosztani, akkor biztosan nem veszít egyik párt se mandátumot, csak a következőt kell kiosztani. Ezt a ház-monotonitásnak (house-monotonicity) nevezzük, ami egy kifejezetten pozitív matematikai tulajdonságnak számít, de számos más módszer nem felel meg ennek a kritériumnak. Ennek azonban ára van: a D’Hondt módszer nem tartja a kvóta-szabályt, azaz egy pártnak több mandátumot is adhat, mint amennyit “felfelé kerekítve” kapna. Pl. ha kerekítés nélkül az eredeti osztóval (=kvóta) egy párt 9,43 mandátumra jogosult, a D’Hondt módszer időnként akár 11-et is adhat neki - pedig kvóta-szabályból az következne, hogy csak 9 vagy 10 mandátum járhatna egy ilyen pártnak (mivel értelemszerűen 9,43-at kerekíteni alapvetően 9-re vagy 10-re lehet, a 11 viszont egy nagy ugrás...).
A D’Hondt módszerről még tudni érdemes, hogy a fentiekből következően (elsősorban a lefelé kerekítés miatt) inkább a nagyobb pártoknak szokott kedvezni, de ha nem kell kerekíteni, akkor mindig az egyértelmű arányos eredményt hozza ki, ilyen értelemben “még” arányosnak nevezzük. Bár a kevésbé torzító (arányosabb…) rendszerekhez képest matematikailag van még egy előnye a D’Hondt módszernek: egy párt sosem járhat jobban azzal, ha kettéválik. Azzal viszont járhatnak jobban pártok, ha összeolvadnak (a D’Hondt ellentétét, amiben ezek pont fordítva vannak, majd külön mutatom be, de most csak elejtem azt az utalást, hogy egy másik amerikai elnök nevén ismert…).
Kérdések otthoni gondolkodásra:
Mitől “működik” a D’Hondt módszer, azaz honnan tudjuk, hogy ez az osztó táblázatos dolog (vagy az osztó csökkentése és lefelé kerekítés) bármennyire is arányos eredményt ad? Mi történne, ha mondjuk 2-vel kezdenénk az osztást?
Pontosan mi számít arányos rendszernek? A D’Hondt módszer minden esetben arányos eredményt ad, ha kerekítésre nincsen szükség, de mi van akkor, ha van szükség kerekítésre (a gyakorlatban majdnem mindig). Honnan tudjuk, hogy akkor mi kellően arányos megoldás? (Van-e erre valamilyen hibahatár?)
Hogyan oldjuk fel a döntetleneket?
A gyakorlatban, ha több kerületet használunk, mikor tekinthetjük a rendszert országosan arányosnak? Melyik az aránytalanabb: ha 53%-47% esetén a rendszer 49%-51%-ot, vagy ha 60%-40%-ot produkál?